Michael Joswig: Current Projects
Tropical mechanism design
Project AA3-5 of MATH+, with Max Klimm. Researcher: Sylvain Spitz
Approximate convex hulls with bounded complexity
Project EF1-3 of MATH+, with Klaus-Robert Müller. Researcher: Marek Kaluba
Moduli spaces of tropical varieties, modifications and compactifications
Project I.9 in SFB/TRR 195, with Hannah Markwig. Researcher: Ayush Kumar Tewari
Central software project: Interaction, high-performance and support
We are currently developing a new computer algebra system, called Oscar. It is written in Julia, and it combines GAP, Singular, polymake and Antic.
Project II.1 in SFB/TRR 195, with Mohamed Barakat, Wolfram Decker, Claus Fieker and Frank Lübeck. Researchers: Reimer Behrend, Sebastian Gutsche, William Hart
polymake: polyhedral data, quotients and stacks
Project II.4 in SFB/TRR 195. Researcher: Lars Kastner
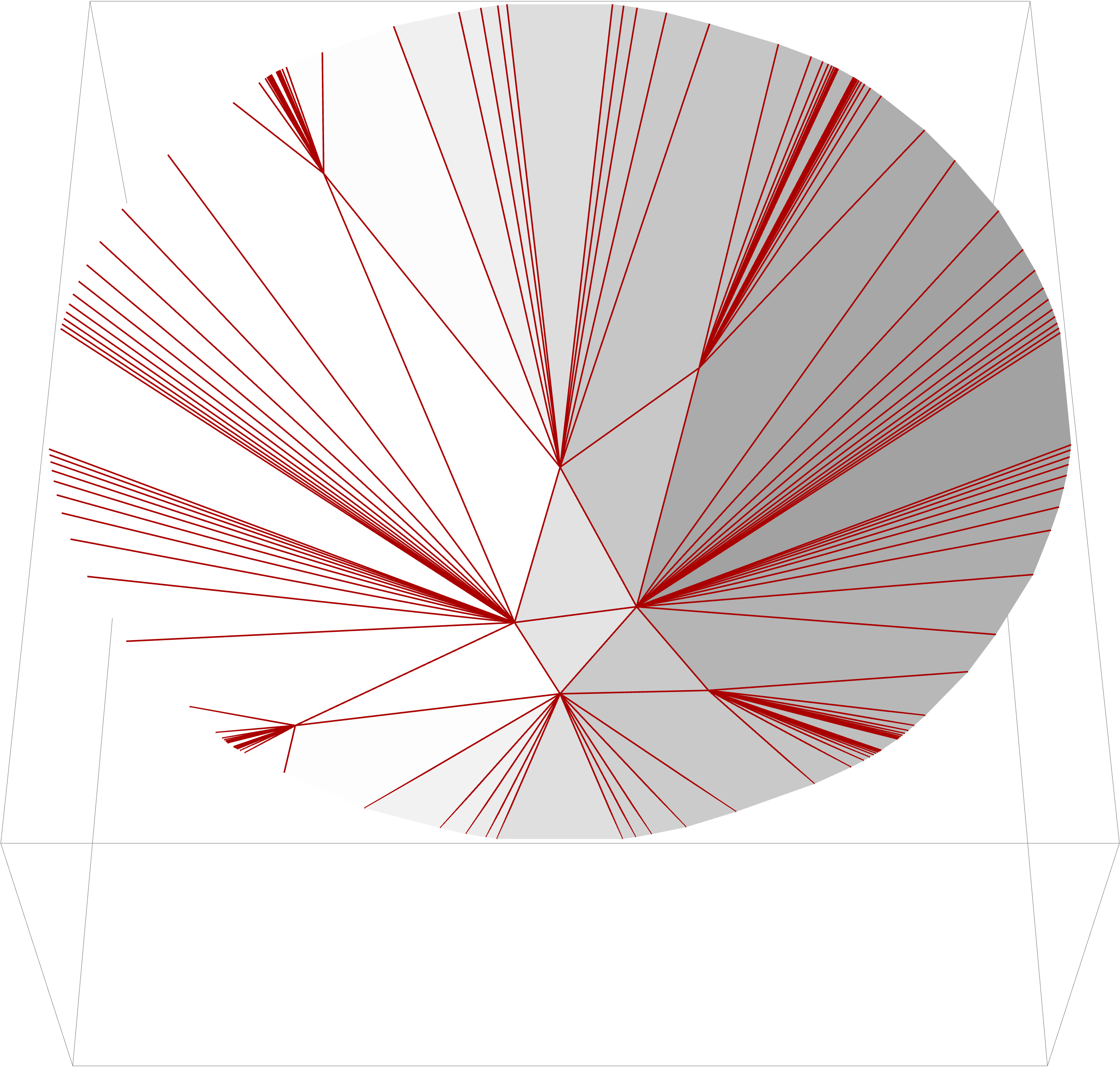
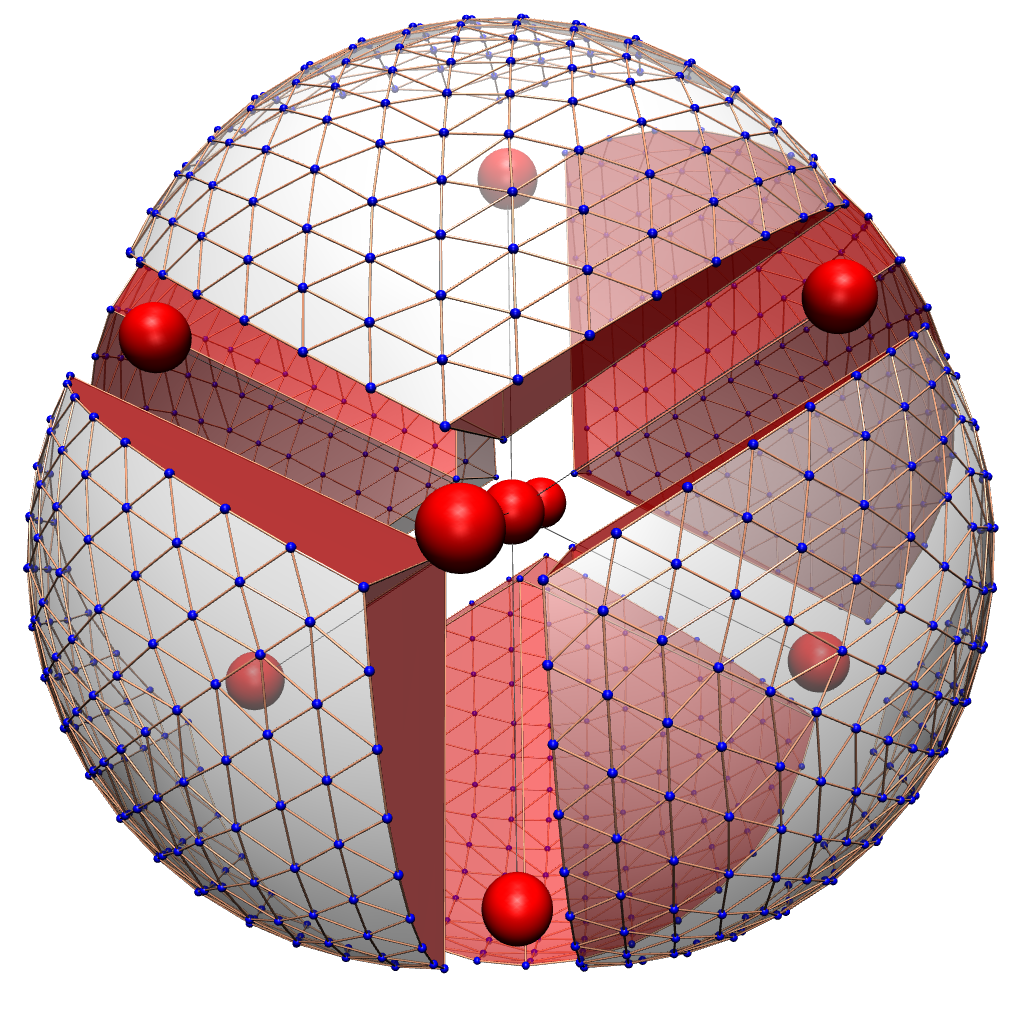
Secondary fans of Riemann surfaces
A famous construction of Gelfand, Kapranov, and Zelevinsky associates to each finite point configuration in Rn its secondary fan, which stratifies the space of height functions by the combinatorial types of coherent subdivisions. A completely analogous construction associates to each punctured Riemann surface a polyhedral fan, whose cones correspond to the ideal tessellations of the surface that occur as horocyclic Delaunay tessellations in the sense of Penner's convex hull construction. We suggest to call this fan the secondary fan of the punctured Riemann surface. The purpose of this project is to study these secondary fans of Riemann surfaces and explore how their geometric and combinatorial structure can be used to answer questions about Riemann surfaces, algebraic curves, and moduli spaces.
Project A11 in the SFB/TRR 109, with Boris Springborn. Researcher: Robert Loewe.
Polyhedral fan structures in toric and tropical geometry
A polyhedral fan is formed of polyhedral cones which meet face to face. Prominent examples include the normal fan of a polytope (which encodes everything there is to say about that polytope from a linear optimization point of view), the secondary fan of a point configuration (which stratifies the regular subdivisions of the convex hull, using the given points), Project in the DFG Priority Program SPP 1489. Researcher: Simon Hampe.
Multiview geometry for ophthalmic surgery simulation
A fundamental problem in machine vision asks to generate geometric information about a scene in 3-space from several camera images. This is relevant, e.g., in the context of augmented reality frameworks for eye surgery simulation. It is the goal of this project to apply techniques from geometric combinatorics and algebraic geometry for analyzing the picture space to allow for a profound computational preprocessing.
Project CH03 in the Einstein Center for Mathematics Berlin. Researcher: André Wagner.
- Rigid Multiview Varieties, Int. J. Algebra Comput. 26 (2016) (with Joe Kileel, Bernd Sturmfels and André Wagner) [Macaulay2 code]
- Conference: Algebraic Vision, TU Berlin, 8-9 Oct 2015.